The first hour of the lab will be devoted to this Sketchpad lab. You will likely have work left to do later. The second part will be an introduction to Kaleidomania.

You have explored double line reflection in other labs and seen how repeated reflections can form a symmetric pattern. In this section we will experiment just a bit more with more attention to the angle between mirrors.

In a new sketch, draw a line AB and then construct a new point B' by rotating B with center A by angle 30 degrees. Let m = line AB and n = line AB'. Let M = reflection in m and N = reflection in n.

Form a shape S (a blob) and reflect this shape over lines m and n to form M(S) NM(S), MNM(S), NMNM(S), etc. and also N(S), MN(S), NMN(S), etc., until no new shapes appear. Count the shapes. Also, reflect lines m and n in the same way to get new lines. Notice that these are lines of symmetry of the figure.

Tell what dihedral group is the symmetry group of this pattern (your answer should be D_n, where n is the number of mirror lines.). How is n related to the angle 30 degrees?

Repeat the same experiment with a new angle.

In a new sketch, draw a line AB and then construct a new point B' by rotating B with center A by angle 40 degrees. Let m = line AB and n = line AB'. Let M = reflection in m and N = reflection in n.

Form a shape S (a blob) and reflect this shape over lines m and n to form M(S) NM(S), MNM(S), NMNM(S), etc. and also N(S), MN(S), NMN(S), etc., until no new shapes appear. Do the shapes "match up" when you go around one time as they did in Experiment 1?

Count the shapes. Also, reflect lines m and n in the same way to get new lines. Notice that these are lines of symmetry of the figure.

Tell what dihedral group is the symmetry group of this pattern (your answer should be D_n, where n is the number of mirror lines.). Explain how n is related to the angle 40 degrees?

Hint for Explanation. The isometry NM is a rotation with center A, so it is A_t, a rotation by t degrees. Then each of the powers (NM)^k are also rotations. Make a table of these rotations for k = 1, 2, 3, … until you get the identity. Explain how you can figure out the number of rotations needed. Now for each rotation in the list, M(NM)^k is a line reflection. How many line reflections are there and how many rotations in the symmetry group?

The first part of this exercise will be to create some examples of repeating symmetric patterns from an original square "tile". The second part will be an analysis of the symmetries of each pattern.

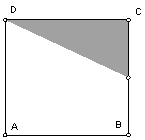
In a new sketch, construct this pattern by constructing a square and shading in the triangle with vertices at C, D and the midpoint of BC. Save this sketch. You will use it as the basis of several experiments.

In a new sketch, copy the figure from above and paste into the new sketch. Now mark segment AB as vector and translate the whole figure. Select the two shaded interiors (no points or segments!) and Define Transform with name T_AB.

Now mark segment BC as vector and translate point A to get a new A'. Select A and A' and Define Transform as T_BC. The two custom transforms are in the Transform menu and can be selected using Control-1 and Control-2.

• Translate the whole figure by BC.
• Then translate the whole figure by AB.
• Continue until the window is fairly full and a pattern emerges. You may want to resize ABCD.

You can do this on the screen or by printing it out, but BE SURE TO CHOOSE "Scale to Fit Page" if you do this. Assume the pattern is continued "to infinity".

• What are the centers of rotational or point symmetry?
• What are the vectors that define translations that are symmetries of this pattern?
• What are the lines of mirror symmetry or invariant lines of glide symmetry?

In a new sketch, copy the figure from above and paste into the new sketch. Now mark segment AB as mirror and reflect the whole figure. Select the two shaded interiors (no points or segments!) and Define Transform with name R_AB.

Now mark segment BC as mirror and reflect point A to get a new A'. Select A and A' and Define Transform as R_BC. Continue in the same way naming reflection across side CD and side DA so that the four custom transforms are in the Transform menu and can be selected using Control-1 through Control-4.

• Reflect the whole figure across BC.
• Then reflect the whole figure across CD. Then reflect across DA.
• Continue until the window is fairly full and a pattern emerges. You may want to resize ABCD.

You can do this on the screen or by printing it out, but BE SURE TO CHOOSE "Scale to Fit Page" if you do this. Assume the pattern is continued "to infinity".

• What are the centers of point symmetry?
• What are the vectors that define translations that are symmetries of this pattern?
• What are the lines of mirror symmetry or invariant lines of glide symmetry?

In a new sketch, copy the figure from above and paste into the new sketch. Now mark A as center and rotate the whole figure by 90 degrees. Select the two shaded interiors (no points or segments!) and Define Transform with name A90.

Now mark B as center and rotate point A by 90 degrees to get a new A'. Select A and A' and Define Transform as B90.

Now you can transform using A90 and B90 using Control-1 and Control 2.

• First, rotate the original shape by A90 until nothing new appears.
• Then rotate the whole resulting shape by B90 until nothing new appears.
• Then rotate the whole resulting shape by A90 until nothing new appears.
• Continue until the window is fairly full and a pattern emerges. You may want to resize ABCD.

You can do this on the screen or by printing it out, but BE SURE TO CHOOSE "Scale to Fit Page" if you do this. Assume the pattern is continued "to infinity".

• What are the centers of 90-degree rotational symmetry?
• What are the centers of point symmetry that are not also centers of 90-degree rotational symmetry?
• What are the vectors that define translations that are symmetries of this pattern?
• What are the lines of mirror symmetry or invariant lines of glide symmetry?

In a new sketch, copy the figure from above and paste into the new sketch. Now mark A as center and rotate the whole figure by 90 degrees. Select the two shaded interiors (no points or segments!) and Define Transform with name A90.

Now mark segment BC as mirror and reflect point A to get a new A'. Select A and A' and Define Transform as R_BC.

Now you can transform using A90 and R_BC using Control-1 and Control 2.

• First, rotate the original shape by A90 until nothing new appears.
• Then reflect the whole resulting shape by R_BC until nothing new appears.
• Then rotate the whole resulting shape by A90 until nothing new appears.
• Continue until the window is fairly full and a pattern emerges. You may want to resize ABCD.

You can do this on the screen or by printing it out, but BE SURE TO CHOOSE "Scale to Fit Page" if you do this. Assume the pattern is continued "to infinity".

• What are the centers of 90-degree rotational symmetry?
• What are the centers of point symmetry that are not also centers of 90-degree rotational symmetry?
• What are the vectors that define translations that are symmetries of this pattern?
• What are the lines of mirror symmetry or invariant lines of glide symmetry?

There are more ways to fill the plane with this square pattern, though some may turn out to be the same old ones in disguise. Here are some suggestions.

• Generate the pattern with rotation by point symmetry, placing centers at each of the midpoints of the sides of ABCD.
• Make one transformation rotation by 90 degrees with center A and the second rotation by 180 degrees with center B.
• In the horizontal direction, define a glide reflection with vector AB and mirror line = perpendicular bisector of AD. Add to this translation by AD or else a glide reflection in the vertical direction.