Math 487 Lab, 11/28

Part A. Glide Reflections

1. Defining a glide reflection in Sketchpad from the definition

· In a new sketch, draw a line AB. Select the line and choose Mark Mirror from the Transform menu. Select A, then B and choose Mark Vector AB from the Transform menu. Then reflection in the line can be denoted R and translation by the vector can be denoted T. The transformation G = TR is a glide reflection by definition.

· Now draw a point P in the Sketch. Reflect P by the marked mirror line to get P' and translate P' by the marked vector to get P''. Then P'' = G(P). Construct the segment PP'' and the midpoint M. Notice that M is the intersection of PP'' with line AB.

· To define G as a custom transformation. Hide the intermediate point P'. Select P and P'' and choose Define Custom Transform from the Transform menu. Name this transformation G.

2. The pattern obtained by iterating G(Q)

· For this experiment we want to the Sketch to look empty. Select All and Choose Hide/Show buttons from the Edit>Action Button menu. Double click on the Hide Button to hide everything.

· Now draw a new point Q and construct Q1 by applying G to Q from the Custom Transform part of the Transform menu. Draw the segment QQ1. Also construct the midpoint of the segment.

· Now select Q1 and the segment and the midpoint all three. From the keyboard hit Control-1 several times to apply G multiple times.

· What does the pattern look like? In particular, notice the arrangement of the midpoints, both the line and the spacing. Draw a line (not a segment) through two of the midpoint. Move Q around; does the midpoint line move? Construct the line through Q parallel to the midpoint line. What other points are on this line? The transformation GG is a translation. Can you see this from the picture? What happens to the figure when you move Q so that it is on the midpoint line?

· Finally, double-click the Show button to make the line AB appear. How is this line related to the figure constructed from Q?

3. A strip (frieze) pattern generated by a glide reflection

· In this experiment, again, we wish the sketch to appear empty, so first use the Hide button to hide the line AB and first set of objects. Then select all of the figure still showing and make new Hide/Show buttons and hide the rest of the figure.

· Now, make a "blob" E as you have done before, i.e., any polygonal shape that you like. The apply G repeatedly as you did in 2 above. (Control-1 makes it fast.)

· This will form a repeated pattern. If you image the pattern extended by translation in both directions infinitely, you get a pattern F whose symmetries include all powers of G. (In practice, your pattern will only move in one direction from the original E; if you want to move in the other direction, you will need to define the inverse of G also.)

· This is an example of a Frieze Pattern. A Frieze Pattern in the plane is a figure whose symmetries include translation by one-nonzero vector v (and hence also all integer multiples mv). But to be a frieze pattern, there cannot be any translations that are not parallel to v.

4. Generating such a frieze pattern with squares

· Make (or choose from the Sketchpad samples) a script to construct a square from an edge AB.

· Then use this to make a pattern like this. If you imagine this being extended forever in both directions, what are the symmetries? In particular, what glide reflections are symmetries? Construct the invariant line of one glide reflection symmetry.

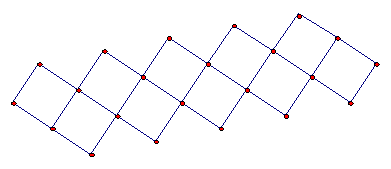
· Once you have figured out exactly which mirror line and translation to use, make a shape E in one of the squares and fill the other ones using the glide reflection.

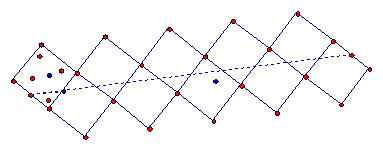
5. A glide reflection from a line reflection and a 90-degree rotation

We have learned that any triple line reflection is a glide reflection (unless the 3 lines are concurrent or parallel).

· In a new sketch, draw a point A and a line m. Let A_90 be rotation by 90 degrees with center A and let R_m be reflection in M. In this experiment we will study D = R_m A_90.

· Pick a point Q and rotate Q by A_90 to get Q' and then get Q'' = R_m(Q'). Hide Q'.

· Choose Q and Q'' and define a custom transform D.

· Draw segment QQ'' and its midpoint M. Then apply D several times to the segment, Q'' and the midpoint M. You should see the same pattern that you found for a glide reflection in your earlier experiment.

· Now we will use the approach of mirror adjustment to see exactly what glide reflection is D.

· A_90 is double reflection R_b R_a in lines through A where the angle between the lines is 45 degrees (why?). Choose b to be the line through A perpendicular to m. Then construct a through A making the correct 45 degree angle (be sure to choose correctly between counterclockwise and clockwise).

· Now D = R_m R_b R_a = B_180 R_a, where B is the intersection of m and b. We know that this is a glide reflection with invariant line through B perpendicular to a. Construct this line d and compare with your Q figure to see that this is correct.

· Finally, rotate the line m around A by multiples of 90 degrees to form a square with center A. How is the line d related to the square. How does this compare with the invariant line in Experiment 4?