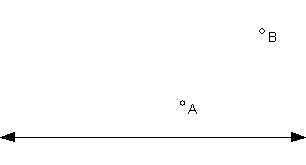
Given a line and two points A and B on the same side of m, construct all circles through A and B that are tangent to m.

Construct all the circles through A and B. Specifically, construct the perpendicular bisector of A and B and construct a (random) point C on this bisector. Now construct the circle c through A with center C.
Drag C back and forth and make a conjecture about how many circles through A and B are tangent to m. (Note: There is one special case (in theory). In practice, it is easy to position your figure so that the circles are too big to handle on the screen, so make adjustments so that you can see what is going on.
Continue with the previous sketch. Try to put the tangents in the picture this way. Let the point P be the intersection of line m and line AB. Construct two points S and T on the circle c so that PS and PT are tangents to c through P.
Now Trace the points S and T as you drag point C (you may want to color these points). What shape to you see?
Construct the shape that you saw as the trace (There is a hint below if needed.) This object intersects line m at points U and V. How can you use U, A, and B to construct one of the tangent circles? How can you use V, A, and B to construct the other tangent circle?
Hint: the object is the circle d with center P through T.
Turn off all the traces. Color the circle c and trace this circle. Notice that c is always orthogonal to circle PT.
Also, notice that B is the inversion of A in the circle d.
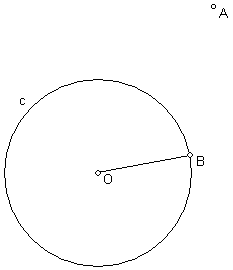
Given a circle c with center O through B and a point A, construct the circle d through A and B that is tangent to circle c at B. Also construct the circle e through A and B that is tangent to line OB at B.
Draw a triangle ABC and construct the circumcircle c of ABC. Now reflect the whole figure line AC. What kind of figure is ABCB'?
In general the circle c and the circle c' will be distinct. Move B so that the circles coincide. Where is the center of c when c = c'? When this happens, how is the line AC related to the circle. What is special about triangle ABC when this happens.
Now construct the angle bisector of angle ABC. Let I be the point of intersection of the angle bisector and segment AC. Construct a circle with center I that is tangent to line AB. What do you see? How can you explain it? Note: If you drag point B so that angle BAB' is great than 180 degrees, then funny things happen with this circle. You have to extend the sides to lines to see what is going on. You can skip this if you like.
Conclusions. What is special about a kite when a circle can be circumscribed about it? Can you prove this? On what line is the center of the circumcircle? Was this clear from the start by symmetry?
Can a circle be inscribed in any convex kite? What does it work? Way are all the angle bisectors concurrent. Try to use the word symmetry in your thinking.
More: Consider inscribed and circumscribed circles for other special
quadrilaterals?
Composing Isometries
There is a large number of possible combinations here. You have explored some before (which you should review).
However, here are some interesting ones that come out of the recent homework
Given points A and B, let T = the product of two rotations: B_240 A_120.
Use Sketchpad to construct T as the product of 1, 2, or 3 line reflections and tell as precisely as possible what the isometry is.
Answer the same question for S = B_120 A_120.
Based on your work, in this figure indicate the image by T of A, B, C. Also, indicate the image by S of A, B, C.
Finally,
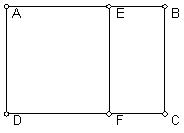
Let ABCD be a rectangle, with a point E on AB and a point F on CD so that AEFD is a square and BCFE is a rectangle similar to ABCD. Prove what is the ratio of the sides of the rectangle ABCD. (The figure below is NOT the right shape, since ABCD is not similar to BCFE, but is shows the setup, just not the correct proportions.)
In this figure, assume that |OB| = 5 and |OA| |OC| = 25. If |AB| = 7, what is |BC|? You should note the connection to inversion, but you don't need inversion to solve this problem.
This is connected to the problem of inscribing circles in trapezoids. Given
trapezoid ABCD with two parallel sides AB and CD, let I be the intersection
of the angle bisectors of angle BAD and angle ADC.
· Show that angle AID is a right angle.
· Show that the point I is equidistant from line AB and line CD.
·
Construct a circle tangent to line AB, CD and AD. 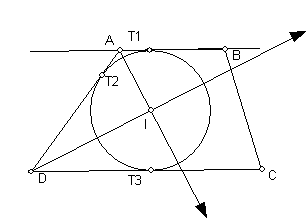
Challenge: Given the tangent point T1, T2, T3 as in the figure, let a = |AT1| and let b = |DT3|. If the radius of the circle is r, what is the relationship between a and b?