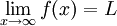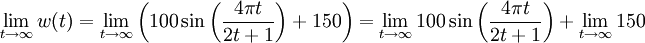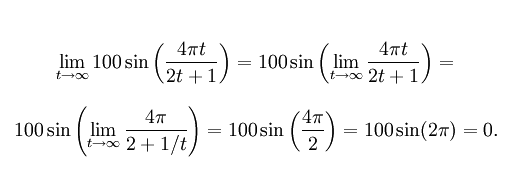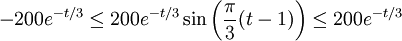Some thoughts on the week 3, part 6 homework in Math 124
We are given two parametric functions defining the populations of
wolf and caribou over time.
Parts (b) and (c)
To study the population of wolves, it helps to study the function
f(t) = (4 π t) /(2t+1) (i.e., the function inside the sin function in
w (t)).
We can rewrite f(t) as f(t) = (4 π )/(2 +1/t).
Writing it this way, we can see that as t gets bigger,
2+1/t gets smaller, and hence f(t) gets bigger.
On the other hand, f(t) is always less than 2 π, and, in fact, the
limit as t approaches infinity is 2 π.
We can see all of this if we look at the graph of f(t):
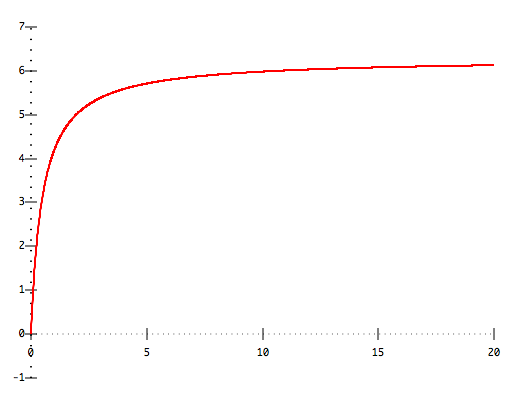
What this tells us is that to make sin (f(t)) as big as possible, we
need f(t) to be equal to π/2 (the value at which sin x is as
big as it gets on the interval 0 ≤ x ≤ 2 π).
Similarly, to make sin (f(t)) as small as possible, we need
f(t) to be equal to 3 π/2.
Part (d)
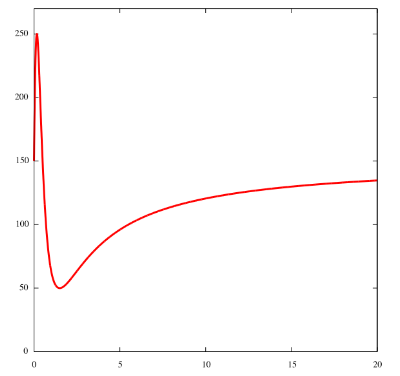
Plotting the wolf population, we have:
Plotting the caribou population, we have:
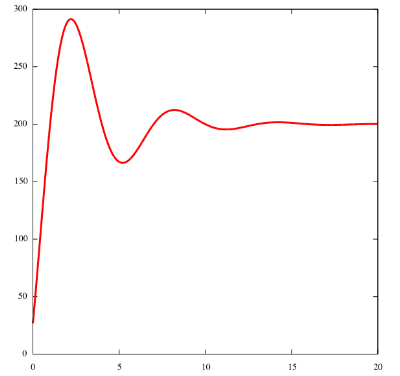
We can see that after some initial drastic wobbling, each population starts settling down
on a value.
Take a look at the graph given in the problem: can you see the same initial
wobbling and then a gradual settling down?
We say that a function f(x)
has a limiting value L if
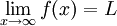
In the case of the wolves, we can find this limiting population like this:
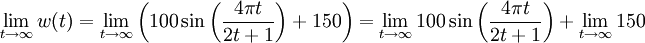
The second limit in the sum is equal to 150.
The first limit we can evaluate using the fact that
sin x is a continuous function for all x.
This allows us to say that the limit of sine of anything is sine of the limit
of that thing: with this, we get
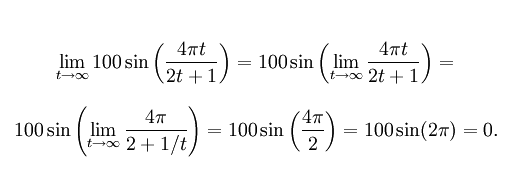
Hence, the limiting population of the wolves is 0+150 = 150.
For the limiting population of the caribou, we use two facts:
- sin x is continuous everywhere,
- the Squeeze Law.
Since -1 ≤ sin x ≤ 1, we have
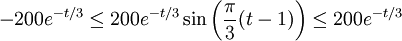
The Squeeze Law then says that if the limits as t approaches infinity
of the expression on the left and right in the inequality above are the same value,
then the limit of the expression in the middle is that value.
That is, if the limit as t approaches infinity of -200e-t/3 equals K,
and the limit as t approaches infinity of 200e-t/3 equals L,
and K=L, then the limit as t approaches infinity of c(t) equals L, too.
By evaluating those limits, you can determine the limiting value of the caribou population.
back to Dr. Conroy's math department page