Thales Theorem and Figure
A key and frequently-occurring figure in the theory of similar triangles is
a figure with two parallel lines adn two intersecting transversals. In this
course we will refer to this figure as a Thales Figure, in honor of the early
Greek geometry who allegedly measure the height of the Great Pyramid using shadows.
Thales Theorem
Given two lines AB and CD. When AC and BD intersect at a point E, and when
E is either (1) a point interior to both segment AC and segment BD or else (2)
exterior to both segments, then the triangles AEB and CED (1) share the angle
AEB = angle CED or else (2) these two angles are vertical angles. Then for such
a figure,
- Line AB is parallel to line CD if and only if
- Triangle AEB is similar to triangle CED if and only if
- EC/EA = ED/EB
Proof: This is BG problem 4.3 (in Assignment 4), except that this problem
is not quite correct as stated, since it is false if E is interior to segment
AC and exterior to segment BD.
Comment: The theorem is true as stated in BG if we allow NEGATIVE
RATIOS of segments when the oriented segments point in opposite directions.
Then the two ratios are positive in case (1) and negative in case (2) and the
theorem is true as stated in BG without assuming (1) and (2) above.
Thales Figure
If any of these conditions (and hence all of these conditions) is true, then
we call the figure a Thales figure. These figures show cases (1) and (2). Interactive
Java Sketchpad figures that show the signed ratio are at this
link.
|
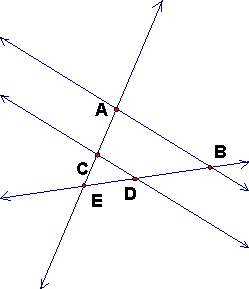
A and C are on the same side of E.(and thus B and D are on the same side
of E). Another way of saying this is that C is on ray EA or that ray EA
= ray EC.
In this case EC/EA > 0 and ED/EB > 0.
|
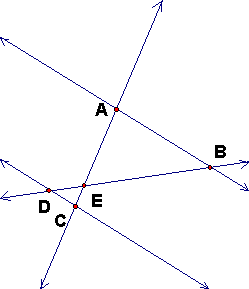
The interesection E is between A and C (and thus between B and D). Another
way of saying this is that the rays EA and EC are opposite rays.
In this case EC/EA < 0 and ED/EB < 0.
|
|
|
 |

