Total angle sum for pentagon = 3*180 = 540 degrees. So each vertex angle = 540/5 = 108 degrees.
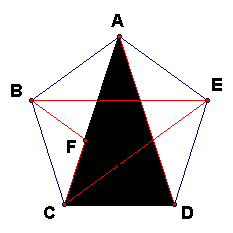
Two sides and a vertex form an obtuse isosceles triangle, two such are shaded here.

Since obtuse vertex angle EAB = 108 and two equal base angles have sum = 180 – 108 = 72, acute base angles such as CAB = 36 degrees.
Also, angle CAD = angle EAB - 2*36 = 36 degrees, so the 2 diagonals from a vertex such as A trisect the vertex angle; that is, they divide the vertex angle into 3 equal 36-degree angles.
Finally, triangle DAC is isosceles since each of the base angles ACD and ADC are equal to 108 – 36 = 72 degrees.
If all 5 diagonals are drawn in the regular pentagon are drawn, these 5 segments form a star shape called the regular pentagram.
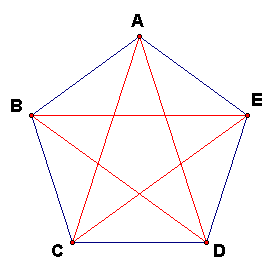
Putting together what is now known about equal angles at the vertices, it is easy to see that the pentagon ABCDE is divided into 5 isosceles triangles similar to the 36-108-36 degree triangle ABC, 5 isosceles triangles similar to the 72-36-72 degree triangle DAC, and one regular pentagon in the center.
There are several ways to see that the diagonal BE is parallel to CD and that CDEB is an isosceles trapezoid. If we assume the knowledge about the angles developed above, there are a couple of quick ways to see this.
Transversal and Supplementary Angle Method: The line BC is a transversal of CD and BE. Angle DCB = 3*36 and angle CBE = 2*36, so the sum of the angles = 5*36 = 180. Since the angles are supplementary, the lines CD and BE are parallel.
Transversal and Equal Angle Method: The line BD is a transversal of CD and BE. Angle BDC = 36 and angle DBE = 36. These congruent alternate interior angles imply that the lines CD and BE are parallel.
Isosceles Triangle Line Symmetry Method: Since the triangle EAB is isosceles, the angle bisector line of angle EAB is the perpendicular bisector of segment BE. Since the triangle DAC is isosceles, the angle bisector line of angle DAC is the perpendicular bisector of CD. But the angle bisector lines of the two angles are the same line (since the bisector of DAC divides angle EAB into two angles of size 18 + 36 degrees). But this means that CD and BE have the same perpendicular bisector. Thus these lines are parallel. Also since BC is the reflection of DE, the segments have the same length.
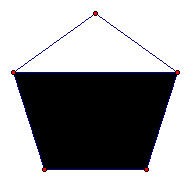
We now know that each diagonal is parallel to one of the sides. So if we draw two diagonals, they make with their parallel side a parallelogram. But since the sides of the regular pentagon are equal, the parallelogram is a rhombus. (Opposite sides are equal in any parallelogram; if two adjacent sides are equal, then all four sides are equal.)
This means that certain lengths inside the star shape are equal to the sides of the pentagon.
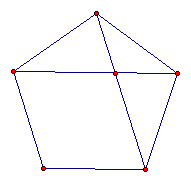
Now we have many ways to find nested, similar isosceles triangles in the pentagram.
We can use these triangles to find the ratio of a diagonal length to a side length of the pentagon. We will take the side length to be the unit length and the diagonal length to be d. Then the ratio will be d with this unit side.
From the rhombus DEAF, we see that AF = FD = DE = DC.
The isosceles triangles DAC and CDF share the base angle ACD = 36 degrees, so they are similar. Triangle DAC has sides AD = AC = d and CD = 1. Triangle CDF has sides DC = DF = 1 and FC = AC – AF = d – 1.
Thus 1/d = DC/AD = FC/CD = (d-1)/1, so 1 = d(d-1), or d^2 – d – 1 = 0.
The positive root of this quadratic equation is (1/2)*(1 + sqrt 5). This is called the Golden Ratio.
For any regular pentagon with side s and diagonal length d, the ratio d/s = the golden ratio.
We have learned how, given a unit length s , to construct the length sqrt 5, so this can be used to construct a length d which is the golden ratio * s.
Then, with s and d, one can start with segment AB and construct all the triangles ABC, ABD, ABE and thus construct a regular pentagon with side AB.
This method also constructs incidentally angles which are 36 degrees and integer multiples of 36 degrees.
Given a center O and a point A, one can construct a regular pentagon ABCDE by drawing the circle with center O through A and then constructing the angles needed (either the central angles such as AOB or the vertex angles).
But the construction of the golden ratio also constructs the needed angles, as was observed in the previous section.