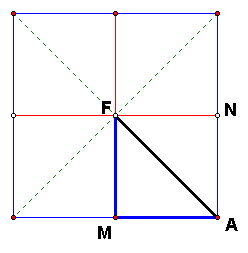
A square has 8 symmetries, 4 line reflections and 4 rotations by multiples of 90 degrees. In this figure the lines of symmetry are the two diagonal lines and the two lines connecting midpoints of opposite sides. These lines break up the square into 8 congruent isosceles right triangles. If we take one of these triangles and transform it by each of the 8 symmetries of the square, the image triangles will fill the square.

This can be seen in a physical experiment by placing two hinged mirrors with their hinge at the center of the square and the two mirrors along two sides of one of the eight triangles, which is colored. Of one looks at the kaleidoscopic image formed by the two mirrors, it appears to be a square of the same color.
Notice that if the square has side length s, the lengths of sides of the triangle are AM = MF = s/2 (blue sides) and AF = (s/2)*sqrt 2 (black side).
The symmetries of a cube of side length s include two kinds of plane reflections.
There are 3 symmetries that are reflections in a plane parallel to a pair of faces of the cube. Each of these 3 planes intersects 4 edges at their midpoints; it is the perpendicular bisecting plane of 4 parallel edges. The symmetry plane cuts the surface of the cube in a square of side s. Each of the planes intersects 4 square faces. It intersects each face along a line of symmetry of the face that connects midpoints of opposite edges. Such a plane contains none of the vertices of the cube.
The other 6 plane reflections are in planes that cut two opposite faces of cubes in diagonals. Such a plane contains two opposite edges of the cube and 4 vertices. Each such plane cuts the surface of the cube in a rectangle of width = s and length = s*sqrt 2.
In the square figure above, if the square is a face of the cube, then two of the 3 planes of symmetry of the first type cut the square along the two lines of symmetry through the midpoints of the sides. Also, two of the 6 planes of symmetry of the second type cut the square along the lines of symmetry that are diagonals of the square. Notice that the former lines are red and the diagonal lines are green.
Compare this with the figure of a cube below. The red segments represent the intersections of the 3 planes of symmetry of the first type with the 3 visible faces of the cube. The green dashed segments represent the intersections of the 6 planes of symmetry of the second type with the 3 visible faces of the cube. Notice that each of these segments is along one of the lines of symmetry of a square face.
Thus these planes cut each face of the cube into the same 8 congruent isosceles right triangles that were the fundamental regions of the symmetries of the square. Since there are six faces, the surface of the cube is cut into 48 congruent isosceles right triangles.
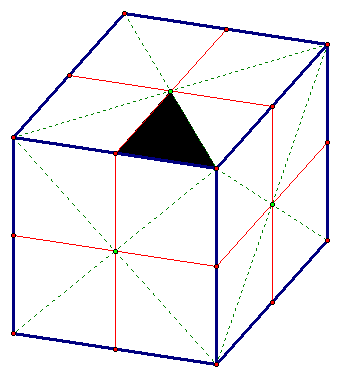
We have seen how the surface of the cube is cut into 48 right triangles by the planes of symmetry of the cube. The interior of the cube is cut into solid polyhedral pieces. Since all the planes of symmetry pass through the center O of the cube, the cube is cut into 48 pyramids with vertex O and with base on of the 48 triangles.
Each pyramid is an irregular tetrahedron. One face is one of the 48 triangles on the faces of the cube. The three other faces are triangles; each has a vertex at O. Each of these faces of the pyramid is a triangle in one of the planes of symmetry of the cube. We can see that one of these planes of symmetry is the type parallel to a pair of faces of the cube. The other two are each planes that contain a pair of edges.
In the figure the vertices of one of the 48 triangles are labeled AFM. Then the faces of the pyramid are triangle AFM (on the face of the cube), triangle OFM (on the plane of symmetry parallel to two cube faces and perpendicular to line AM), triangle OMA (on the plane of symmetry that contains O and line AM) and triangle OAF (on the plane of symmetry that cuts a face in line AF).
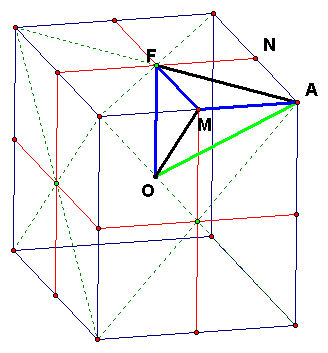
If we examine the edges of the pyramid further, we see that the edge OF is perpendicular to the face AFM.
Also the lengths of 3 edges of the pyramid are equal to s/2; these are AM = MR = FO. Two edges are diagonals of squares, so AF = OM = (s/2)*sqrt 2. The final edge is one half the diameter of the cube OA = (s/2)*sqrt 3 (OA is the diagonal of a "corner cube").
Thus we see that among the four faces of the tetrahedron, there are two pairs of congruent triangles. Two are isosceles right triangles with legs = s/2 and two are right triangles that are halves of the rectangle with width s/2 and length (s/2)*sqrt 2. (Note the color coding of the lengths below and lengths in the figure above.) The parallelogram and rectangle below can be cut out and folded along the indicated diagonal and then attached to form the pyramid.
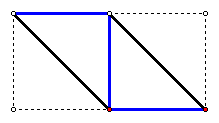

It is easy to check that the volume of one of these pyramids is 1/48 of the volume of the cube.
Finally, there is a physical experiment that shows the symmetries of a cube. One can build a 3D kaleidoscope by joining 3 mirrors in space so that the mirrors form the 3 sides of the pyramid that meet at O. Then if one builds a model of one of the 48 pyramids and drops it into the kaleidoscope, one sees what appears to be a whole cube.