Angle-Side-Angle
Using words:
If two angle in one triangle are congruent to two angles of a second triangle, and also if the included sides are congruent, then the triangles are congruent.
Using labels:
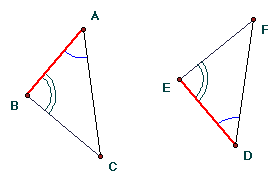
If in triangles ABC and DEF, angle A = angle D, angle B = angle E, and AB = DE, then triangle ABC is congruent to triangle DEF.
Proof:
In the figure, the known congruent segments and angles in triangles ABC and DEF are color-coded.

|
Construct a point F' on ray AC so that AF' = DF. Angle BAF' = angle BAC and this = angle EDF and AB = DE (given), so triangle DEF = triangle ABF'. There are two possibilities for point F': F' is the same as point C or it is not.
QED |
|