Properties of an Isosceles Triangle
Definition: A triangle is isosceles if two of its sides
are equal.
We want to prove the following properties of isosceles triangles.
|
Theorem: Let ABC be an isosceles triangle with AB = AC. Let M
denote the midpoint of BC (i.e., M is the point on BC for which MB = MC).
Then
a)
Triangle ABM is congruent to triangle ACM.
b)
Angle ABC = Angle ACB (base angles are equal)
c)
Angle AMB = Angle AMC = right angle.
d)
Angle BAM = angle CAM
|

|
Corollary: Consequently, from these facts and the definitions:
- Ray AM is the angle bisector of angle BAC.
- Line AM is the altitude of triangle ABC through A.
- Line AM is the perpendicular bisector of B
- Segment AM is the median of triangle ABC through A.
Proof #1 of Theorem (after B&B)
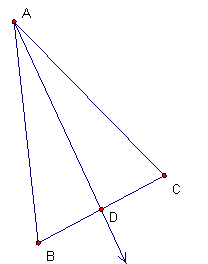
Let the angle bisector of BAC intersect segment BC at point D.
- Since ray AD is the angle bisector, angle BAD = angle CAD.
- The segment AD = AD = itself.
- Also, AB = AC since the triangle is isosceles.
Thus, triangle BAD is congruent to CAD by SAS (side-angle-side).
This means that triangle BAD = triangle CAD, and corresponding sides
and angles are equal, namely:
- DB = DC,
- angle ABD = angle ACD,
- angle ADB = angle ADC.
|
|
(Proof of a). Since DB = DC, this means D = M by definition of the midpoint.
Thus triangle ABM = triangle ACM.
(Proof of b) Since angle ABD = angle ABC (same angle) and
also angle ACD = angle ACB, this implies angle ABC = angle ACB.
(Proof of c) From congruence of triangles, angle AMB = angle AMC. But by
addition of angles, angle AMB + angle AMC = straight angle = 180 degrees.
Thus 2 angle AMB = straight angle and angle AMB = 90 degrees = right angle.
(Proof of d) Since D = M, the congruence angle BAM = angle CAM
follows from the definition of D. (These are also corresponding angles in
congruent triangles ABM and ACM.)
QED*
*Note: There is one point of this proof that needs a more careful “protractor
axiom”. When we constructed the angle bisector of BAC, we assumed that this
ray intersects segment BC. This can’t be quite deduced from the B&B form
of the axioms. One of the axioms needs a little strengthening.
The other statements are immediate consequence of these relations and the definitions
of angle bisector, altitude, perpendicular bisector, and median. (Look them
up!)
Definition: We will call the special line AM the line of symmetry of the isosceles triangle.
Thus we can construct AM as the line through A and
the midpoint, or the angle bisector, or altitude or perpendicular bisector of
BC. Shortly we will give a general definition of line of symmetry that applies
to many kinds of figure.
Proof #2 (This is a slick use of SAS, not presented Monday. We may discuss
in class Wednesday.)
The hypothesis of the theorem is that AB = AC. Also, AC = AB (!) and angle
BAC = angle CAB (same angle). Thus triangle BAC is congruent to triangle BAC
by SAS.
The corresponding angles and sides are equal, so the base angle ABC = angle
ACB.
Let M be the midpoint of BC. By definition of midpoint, MB = MC. Also the
equality of base angles gives angle ABM = angle ABC = angle ACB = angle ACM.
Since we already are given BA = CA, this means that triangle ABM = triangle
ACM by SAS.
From these congruent triangles then we conclude as before:
- Angle BAM = angle CAM (so ray AM is the bisector of angle BAC)
- Angle AMB = angle AMC = right angle (so line MA is the perpendicular bisector
of BC and also the altitude of ABC through A)
QED
Faulty Proof #3. Can you find the hole in this proof?)
In triangle ABC, AB = AC. Let M be the midpoint and MA be the perpendicular
bisector of BC.
- Then angle BMA = angle CMA = right angle, since MA is perpendicular bisector.
- MB = MC by definition of midpoint. (M is midpoint since MA is perpendicular
bisector.)
- AM = AM (self).
So triangle AMB = triangle AMC by SAS.
Then the other equal angles ABC = ACB and angle BAM = angle CAM
follow from corresponding parts of congruent triangles. And the rest is as
before.
QED??

